局部二值模式（英文：Local binary patterns，缩写：LBP）是机器视觉领域中用于分类的一种特征，于1994年被提出。局部二值模式在纹理分类问题上是一个非常强大的特征；局部二值模式是一个简单但非常有效的纹理运算符。它将各个像素与其附近的像素进行比较，并把结果保存为二进制数。由于其辨别力强大和计算简单，局部二值模式纹理算子已经在不同的场景下得到应用。LBP最重要的属性是对诸如光照变化等造成的灰度变化的强健性。它的另外一个重要特性是它的计算简单，这使得它可以对图像进行实时分析。

参考：局部二值模式(Local Binary Patterns)进行纹理分类;局部二值模式–维基百科

一、概念

在最简简化的情况下，局部二值模式特征向量可以通过如下方式计算：

  • 将检测窗口切分为区块（cells，例如，每个区块16x16像素）。
  • 对区块中的每个像素，与它的八个邻域像素进行比较（左上、左中、左下、右上等）。可以按照顺时针或者逆时针的顺序进行比较。
  • 对于中心像素大于某个邻域的，设置为0；否则，设置为1。这就获得了一个8位的二进制数（通常情况下会转换为十进制数字），作为该位置的特征。
  • 对每一个区块计算直方图。
  • 此时，可以选择将直方图归一化；
  • 串联所有区块的直方图，这就得到了当前检测窗口的特征向量。

此特征向量可以通过诸如支持向量机(SVM)等机器学习算法来产生一个分类器。

一个有效的扩展被称为“等价模式”，可用于对特征向量降维，以及实现简单的旋转不变算子。其主要根据是一些模式比另一些模式更加常见。当某个LBP只包含从0到1或从1到0的最多两次跳变时，该LBP被定义为一个等价模式。例如，00010000（2次跳变）是一个等价模式，01010100（6次跳变）不是。在计算LBP的直方图时，对于每一个等价模式都各有一个组（bin），而所有非等价模式都被归类到一个单独的组中。使用等价模式，一个区块的特征长度能从256降到59。

二、特性和纹理分类方法

对于二维的纹理分析，具有很多潜在的应用。例如，工业表层检查，远程监控，生物制药图像分析等等领域。但是在实际应用时，会存在很多问题。主要的问题在于现实世界中的纹理并不像实验中的那么规整，存在着很多变化，例如：

  1. 由于非均匀光源导致的光照变化；
  2. 实际的情况下，物体方向是随机的；
  3. 空间尺度不一致。

而且，很多纹理分类的方法计算复杂度过高，难以实用化。为了解决这些问题，可以采用改进型的局部二值模式进行纹理分类。
改进型的**局部二值模式(Local Binary Patterns)**具有以下优点：

  1. 具有灰度不变性；
  2. 具有旋转不变性；
  3. 能够多分辨率分析；

并且，由于局部二值模式计算复杂度较低，因此，是一种很实用的图像处理方法。这里，我用简单的语言简述一下LBP的各种特性和纹理分类方法。

局部二值模式

首先，我们考虑一幅图像上的一个像素点，以及该像素点的八邻域。如下图(左)所示，我们考虑九宫格内的中心像素点，假设为“6”。周围像素点的数值如图所示。这时，我们将八邻域中，数值大于等于中心像素点的记为“1”，数值小于中心像素点的记为“0”。这时，我们得到下图(右)。这就是基本的局部二值模式(Local Binary Patterns)。之所以叫作“二值”，是因为LBP之后的模式只有0和1两个数值(同理，可以定义三值模式)。

细心的人可能会发现，其实LBP操作相当于：以中心点灰度值做参考，进行局部二值化处理。

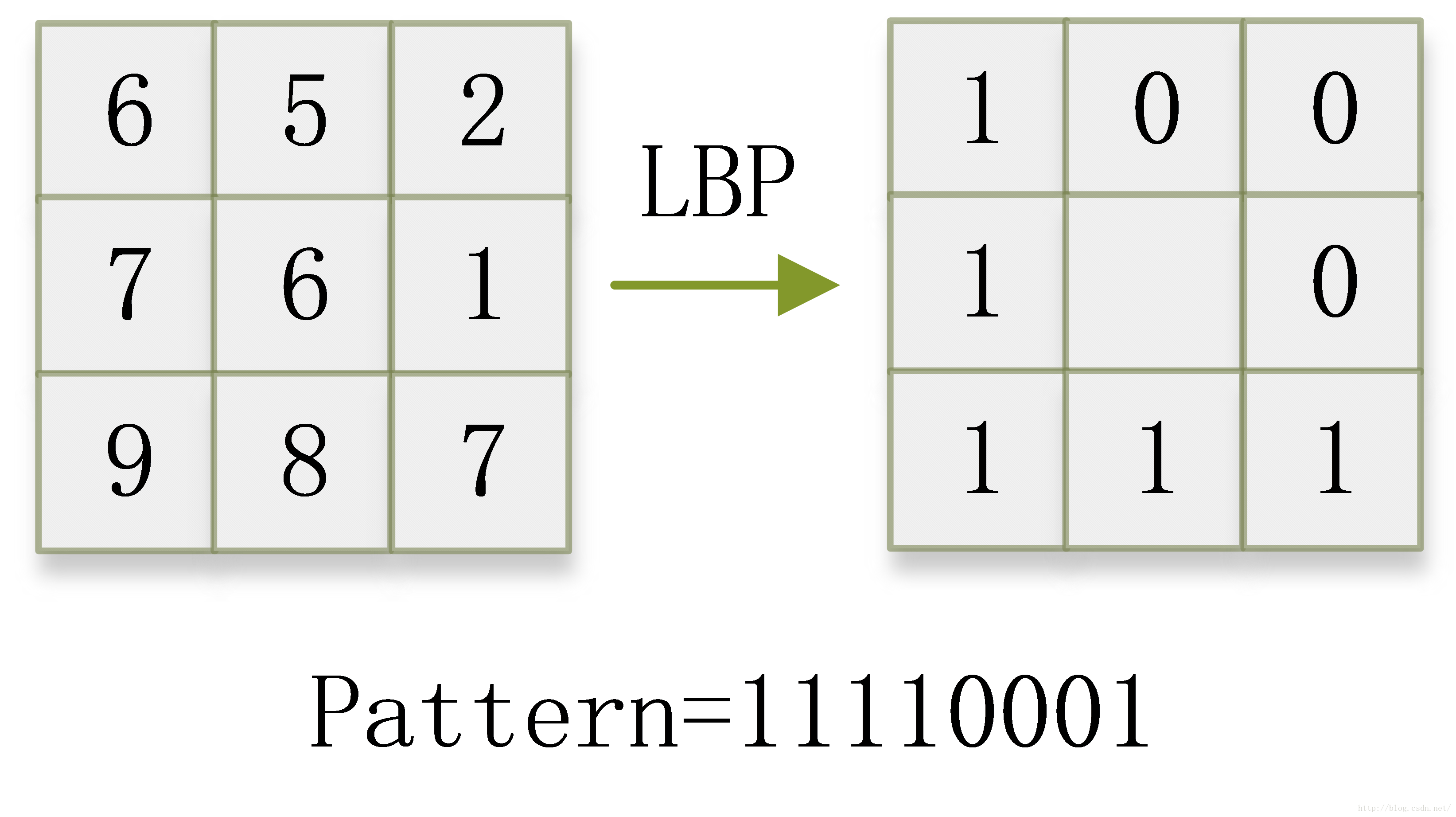
这时，我们定义左边中心像素为起始点，逆时针方向为正方向，然后按顺序数LBP的输出值，便会得到一个LBP编码。这样，我们就称中心像素点的LBP值为11110001。同样，我们对一幅图像的所有像素点进行LBP处理，每个像素点都有一个LBP值，这个值在十进制下介于0到255之间。这样得到的图像称为LBP特征图。

1.灰度不变性

通常，同样的物体具有同样的纹理特征，但不同时间段对物体的照相会因为光照的不同，导致亮度差异很大。但LBP具有灰度不变性的特征，可以抵抗光照变换所带来的影响。

如下图所示，第一幅图像经过LBP变换后得到LBP值为11110001。而第二幅图像的每个像素在第一幅图像的基础上都增加了50，进行LBP变换后，得到的LBP值仍然是11110001。因为LBP特征反应了局部亮度的相对变化，所以整体增加或减少一个值对LBP特征并没有大的影响，因此得到结论：差分分布对平均光强不敏感。

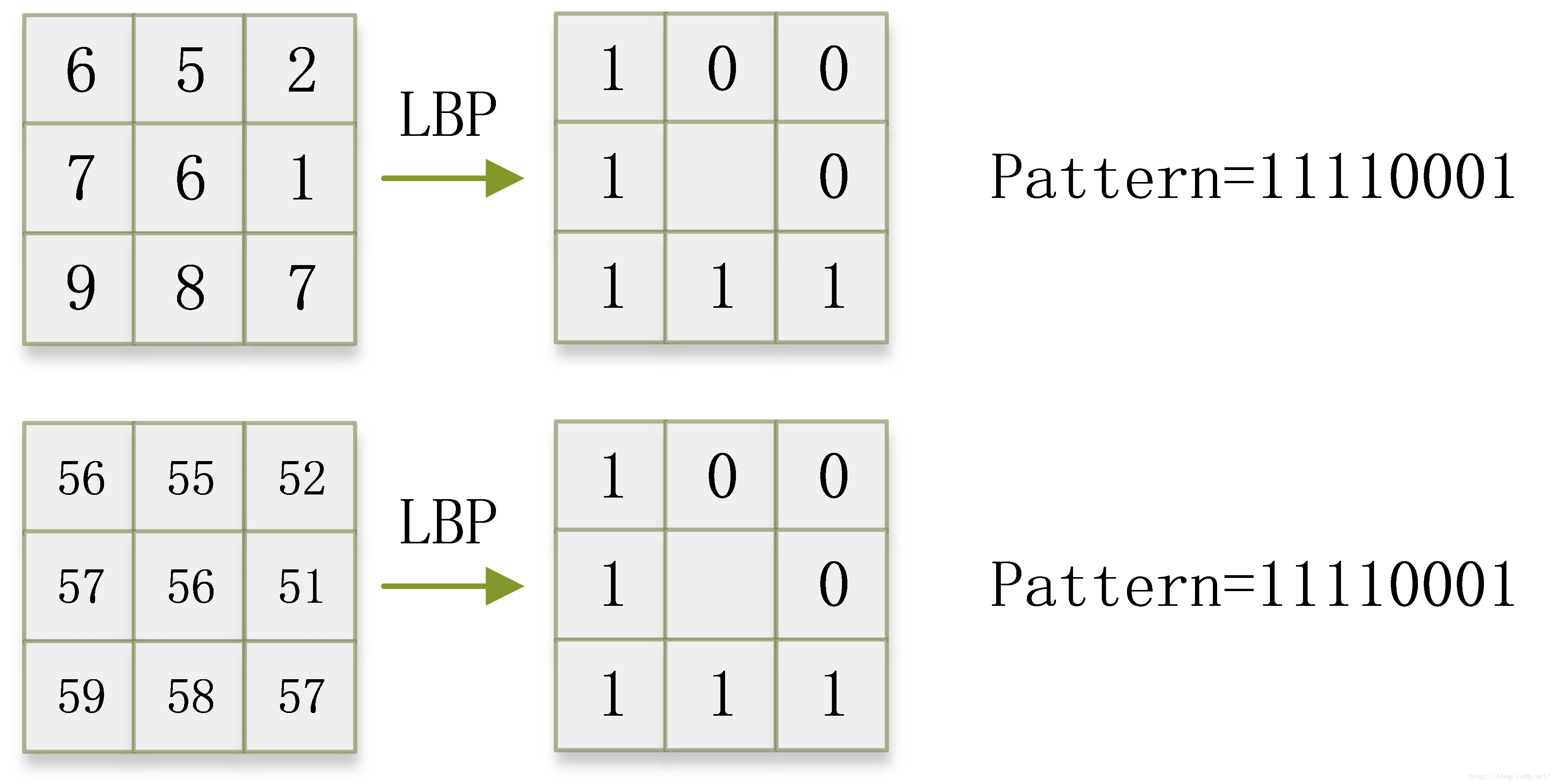
不过值得注意的是，该灰度不变性仅仅适用于灰度值的单调变化，也就是说，光照的变换要是线性的。

2.圆形局部二值模式

为了更加准确的反映纹理的特性，会采用“圆形”的局部二值模式(下面均是如此)。如下图所示，所谓的“圆形”，只是采样点的选择不同于八邻域。它以中心像素点为圆心，R(pixel)为半径画圆，在圆上均匀地选取P个点作为采样点。而后面的处理方法与前面的八邻域LBP方法一致。下图是R=1(pixel)，P=8时的情况。

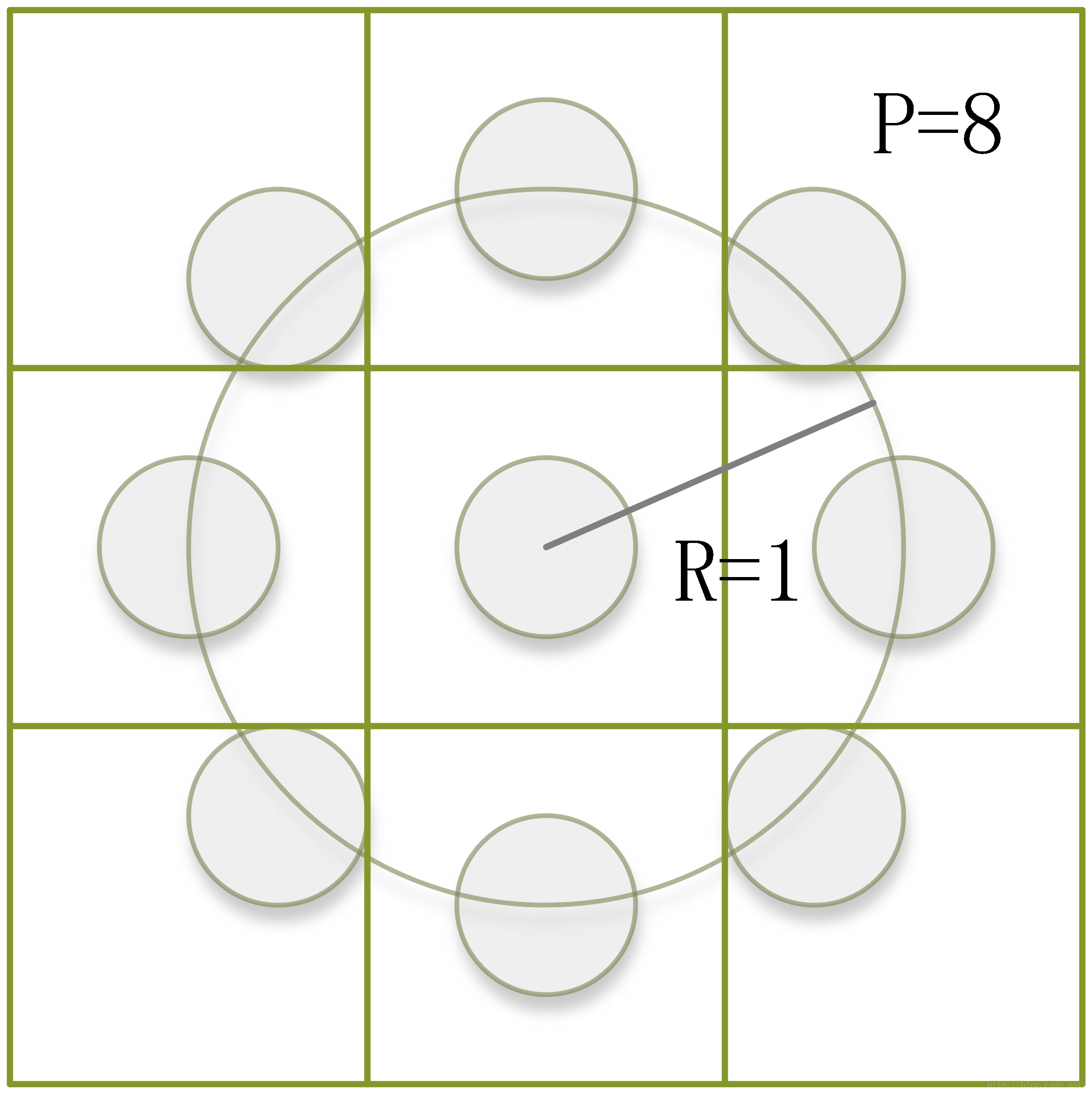
我们可以发现，R的大小决定了圆的大小，反映了二维空间的尺度；而P的大小决定了采样点数，反映了角度空间的分辨率。同样的，我们还可以改变R和P的值，实现不同的尺度和角度分辨率(如下图)。这也是后面“多分辨率分析”的理论基础。

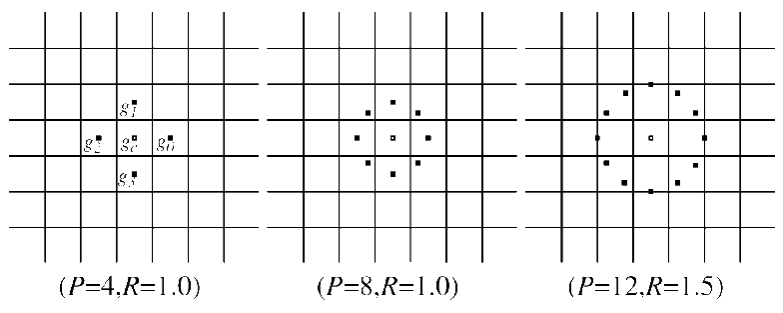
这里值得注意的是：由于采样点在圆上，所以不一定会准确的落在像素点中。因此可能需要对采样点位置进行插值获得采样点的像素估计值。

3.旋转不变性

对于下图的两个模式，其实只有方向不同，在实际中是同一个模式的不同状态。为了克服旋转带来的变化，引入了“旋转不变性”方法。

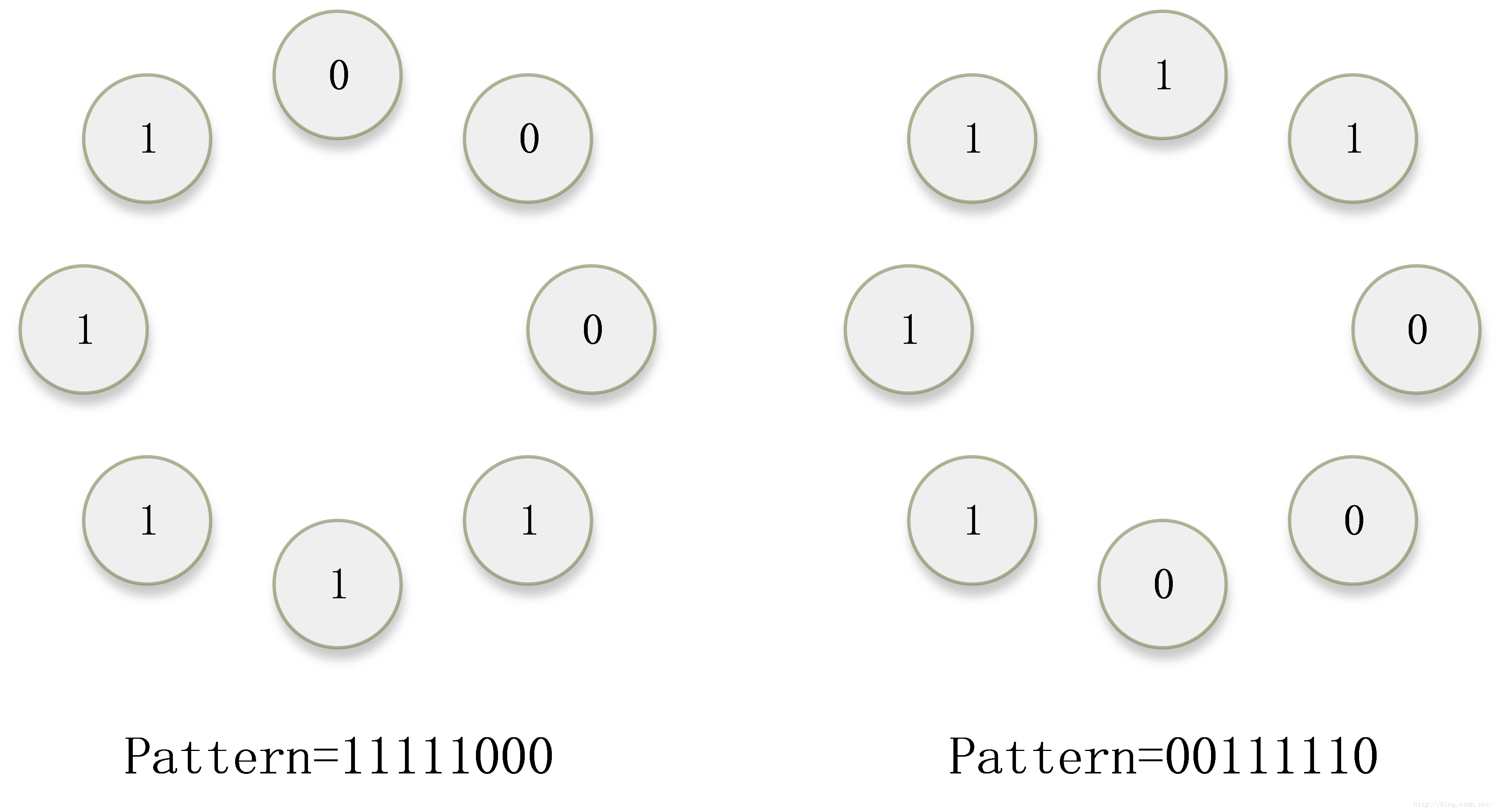
处理方法如下：两种模式各有一个LBP值，将这个LBP值不断的循环右移，并找到一个右移过程中最小的结果，作为新的LBP值。可见，这两种模式得到的新LBP值相同，属于同一种模式，从此解决了方向变化的问题。其中，”循环右移”的实质是对模式图案不断的旋转。”最小化”过程的实质是寻找能量最低的位置。

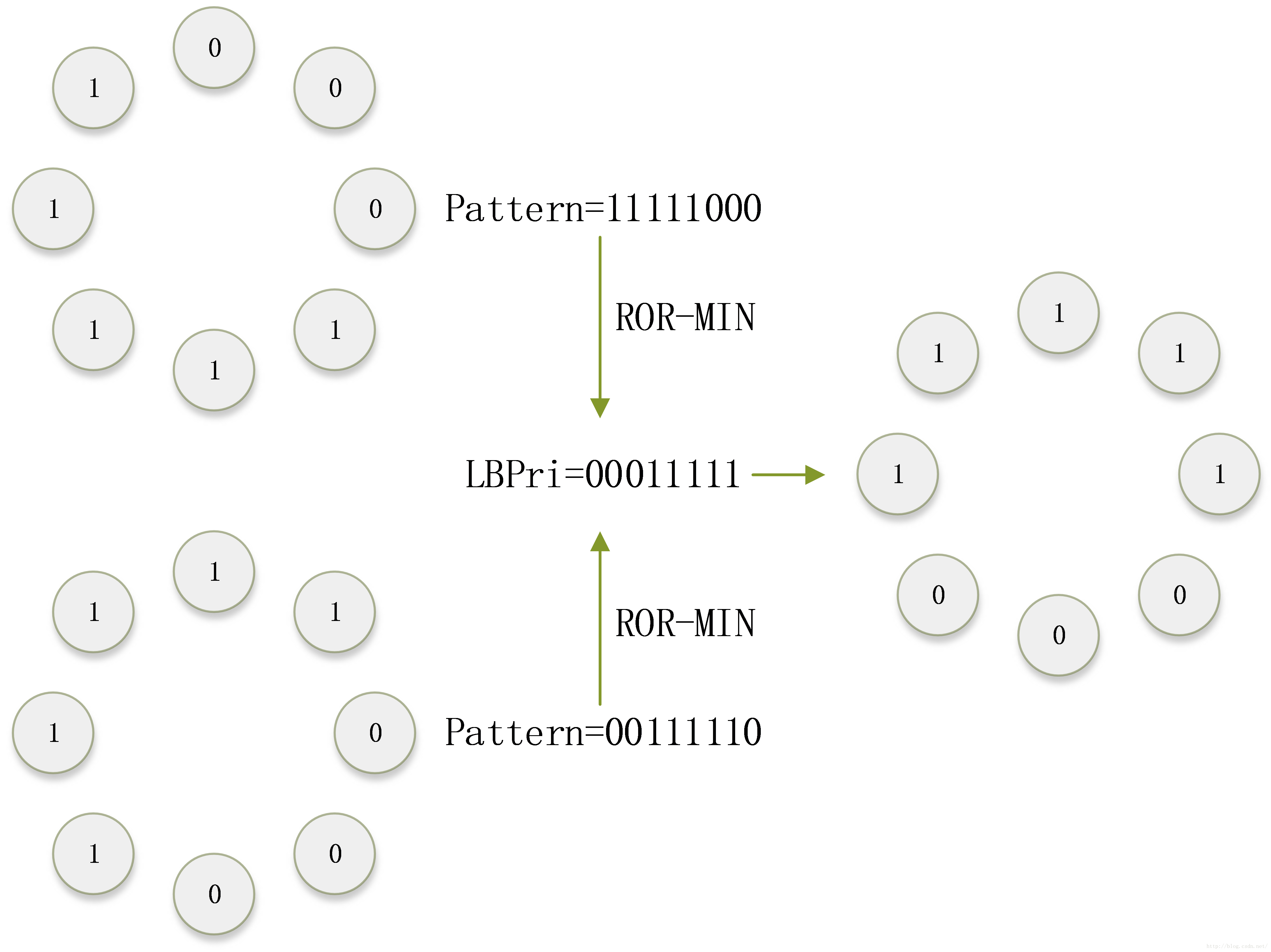
对于P=8的LBP，一共有8个采样点，每个采样点可能输出0或1，所以一共有256种局部二值模式。但其中有一些仅仅是方向不同，通过旋转之后可以重合。通过以上旋转不变性处理之后，256种LBP变为了具有“旋转不变性”的36种模式。如下图所示：(特点是任意两种模式经过任意旋转之后不会重合)

4.增强型旋转不变性

在实际应用中，我们经过统计会发现， 上图中第一行的9种模式最为常见，而后面的27种模式并不常见。如果将后面的27种模式每种单独分类，会因为它们出现概率太小，而具有一定的随机性，因此分类结果反而不稳定。因此，我们要对这种方法进行改进。

我们对每个LBP上的数值按顺序读一圈，将0->1和1->0变化的总次数记为U。对于上图可以发现，第一行模式的U值均小于等于2(反映了平坦或边缘区域)，后面27种模式的U值均大于等于4(变化剧烈，不常见)。如下图。

这样，对于一般LBP进行处理时，我们将U值小于等于2的LBP每个单独分为一类，而对于U值大于等于4的LBP全部归为一类，这样一共有P+2类。

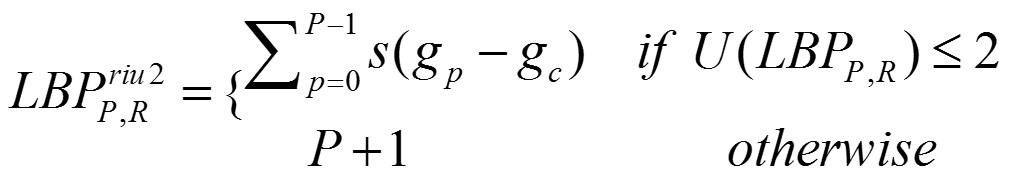
对于P=8的情况下，原先分好的36个LBP就变成了10类。

5.非参数化分类原理

对于一幅图像，每个像素点均可以根据上述方法计算出一个LBP值，从而将这个像素归为(P+2)类中的一类。这样我们可以得到一个特征图，图中每点的数值代表像素点的类别，范围为：**0~(P+1)**。最终的纹理特征即为：LBP类别特征图的输出直方图。

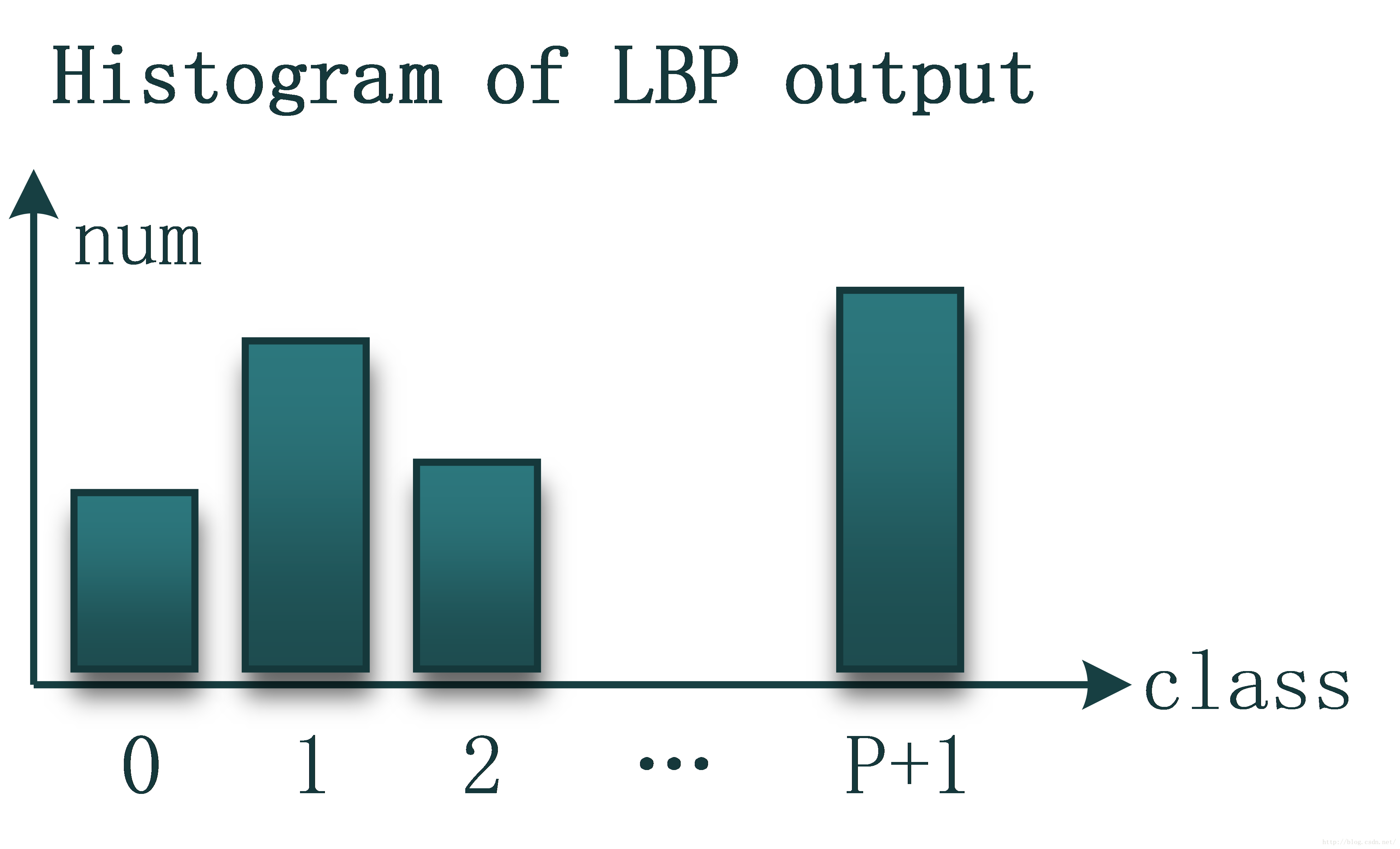
如果，样本图像记为S，待匹配的模型记为M。b代表类别，取值为b=1,2…B，其中B=P+2。

则样本S和模型M的匹配程度，使用**最大对数似然(log-likelihood)**统计方法表示：

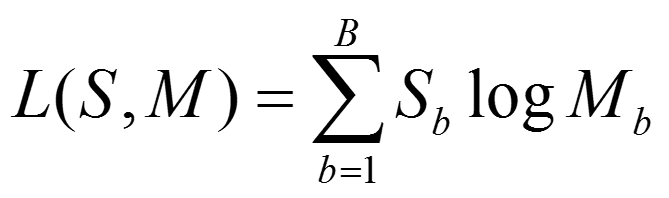
而这个表达式，是如下式子(log-likelihood ratio)的一个简化版本：

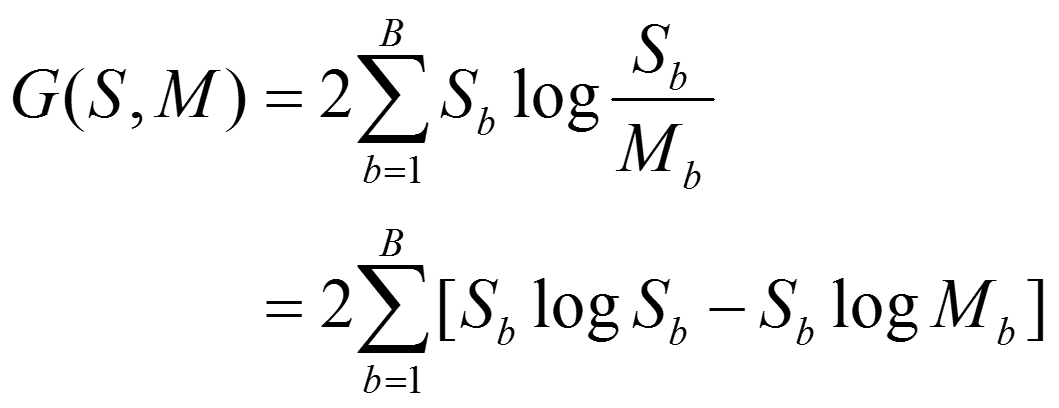
6.多分辨率分析

在前面的第2节，我们提到了多分辨率分析的基础是改变不同的R值和P值，实现不同的二维尺度分辨率和不同的角度空间分辨率。在第5节中交代了非参数分类的原则表达式。多分辨率分析，及改变不同的R值和P值，重复以上操作，最终将总的最大似然统计作为分类准则。如下公式所见，一共完成了N种不同的分辨率测度，最终的似然函数为：

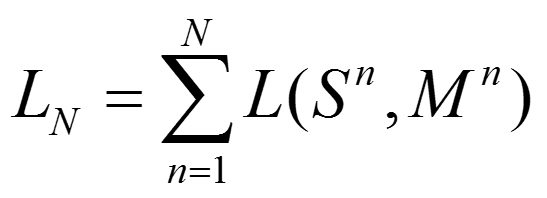
如有任何疑问，欢迎一起讨论。