一些参考资料：

torch.max/eq()…

torch.expand/squeeze()…

torch.contiguous()

torch.gather()

loss funtion

Triplet-Loss原理及其实现、应用

batch-hard-strategy

PyTorch triphard代码理解

三元组怎么挑选？

batch的形成/PK取样

​ 随机的从dataset中取样P个人、每个人取K张图片，比如P=16，K=4，则一个batch中有16*4=64张图片。

构建三元组

​ 由上面得到一个batch中的图片都经过网络提取特征，得到64个特征。接下来构建三元组：

  • 把每一个图片都当成anchor，总共可以选出64个三元组（其实按照排列组合可以选出很多三元组的，In defense of triplet loss这篇文章就只构建有代表性的64个三元组）
  • 每个三元组的anchor选定后，positive从K-1个中选一个与anchor特征距离最远的样本，negative从P*K-K个中选一个与anchor特征距离最近的样本，这样子对这个anchor来说，选出来的positive和negative都是最困难的。这样组建了P*K个三元组，计算出P*K个triplet loss，把这些loss取平均进行反传。

数据集迭代的过程是按照person id来循环的，假设数据集有751个id，一个batch取掉了16个id，这样经过int(751/16)个batch就循环了一次（一个epoch），接下来把id的顺序打乱，进行下一轮迭代（下一个epoch）。

训练方法

offline

  • 训练集所有数据经过计算得到对应的 embeddings, 可以得到 很多<i, j, k> 的三元组，然后再计算 triplet loss
  • 效率不高，因为需要过一遍所有的数据得到三元组，然后训练反向更新网络

online

  • 从训练集中抽取B个样本，然后计算 B 个embeddings，可以产生 B*B*B个 triplets （当然其中有不合法的，因为需要的是<a, p, n>）
  • 实际使用中采用此方法，又分为两种策略 （是在一篇行人重识别的论文中提到的 In Defense of the Triplet Loss for Person Re-Identification），假设 B = P*K , 其中P个身份的人，每个身份的人K张图片（一般K 取 4）
    • Batch All: 计算batch_size中所有valid的的hard triplet 和 semi-hard triplet， 然后取平均得到Loss。
      • 注意因为很多 easy triplets的情况，所以平均会导致Loss很小，所以是对所有 valid 的所有求平均。
      • 可以产生 P K ( K − 1 ) ( P K − K ) 个 triplets
        • PK个 anchor
        • K-1 个 positive
        • PK-K 个 negative
    • Batch Hard: 对于每一个anchor， 选择距离最大的d(a, p) 和 距离最小的 d(a, n)
      • 共有 P K个 三元组triplets

margin的选择？

  • 当 margin 值越小时，loss 也就较容易的趋近于 0，于是 Anchor 与 Positive 都不需要拉的太近，Anchor 与 Negative 不需要拉的太远，就能使得 loss 很快的趋近于 0。这样训练得到的结果，不能够很好的区分相似的图像。

  • 当 margin 值越大时，就需要使得网络参数要拼命地拉近 Anchor、Positive 之间的距离，拉远 Anchor、Negative 之间的距离。如果 margin 值设置的太大，很可能最后 loss 保持一个较大的值，难以趋近于 0 。

torch.nn.MarginRankingLoss()

两个N维向量之间的相似度，用于排序任务，该方法计算两组数据之间的差异，返回一个N*N的loss矩阵

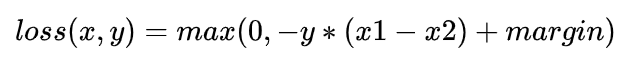
y=1，希望x1比x2大，当x1>x2时，不产生loss

y=-1，希望x1比x2小，当x2>x1时，不产生loss

1
2
3
4
5
6
7
8
9
10
11
x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)

target = torch.tensor([1, 1, -1], dtype=torch.float)  #这是y
loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none') # margin ：边界值，reduction：计算模式
loss = loss_f_none(x1, x2, target)
# y=-1 x1[2]=3  3-2 3-2 3-2 1 1 -1 --->0 0 1
#输出：
loss:tensor([[1., 1., 0.],
        [0., 0., 0.],
        [0., 0., 1.]])

torch.nn.SoftMarginLoss()

二分类logistic损失：

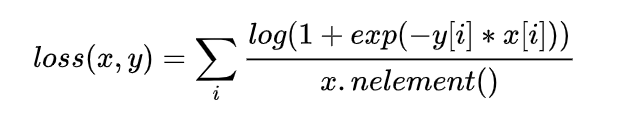
其中，x.nelement()是平均值，y=1或-1

1
2
3
4
5
6
7
inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)

loss_f = nn.SoftMarginLoss(reduction='none')
loss = loss_f(inputs, target)
#输出：
SoftMargin:  tensor([[0.8544, 0.4032],[0.4741, 0.9741]])
1
2
3
4
5
6
idx = 0
inputs_i = inputs[idx, idx]
target_i = target[idx, idx]

loss_h = np.log(1 + np.exp(-target_i * inputs_i))
#输出：tensor(0.8544)