autograd与逻辑回归
autograd 与逻辑回归
1、自动求导 (autograd)
在深度学习中,权值的更新是依赖于梯度的计算,因此梯度的计算是至关重要的。在 PyTorch 中,只需要搭建好前向计算图,然后利用torch.autograd自动求导得到所有张量的梯度。
torch.autograd.backward()
功能:自动求取梯度
- tensors: 用于求导的张量,如 loss
- retain_graph: 保存计算图。PyTorch 采用动态图机制,默认每次反向传播之后都会释放计算图。这里设置为 True 可以不释放计算图
- create_graph: 创建导数计算图,用于高阶求导
- grad_tensors: 多梯度权重。当有多个 loss 混合需要计算梯度时,设置每个 loss 的权重。
retain_graph 参数
代码示例:
1 | w = torch.tensor([1.], requires_grad=True) |
其中y.backward()方法调用的是torch.autograd.backward(self, gradient, retain_graph, create_graph)。但是在第二次执行y.backward()时会出错。因为 PyTorch 默认是每次求取梯度之后不保存计算图的,因此我们第二次求导梯度时,计算图已经不存在了。报错信息提示我们在第一次求梯度时使用y.backward(retain_graph=True)即可。如下代码所示:
1 | w = torch.tensor([1.], requires_grad=True) |
grad_tensors 参数
代码示例:
1 | w = torch.tensor([1.], requires_grad=True) |
结果为:tensor([9.])
该 loss 由两部分组成:$y{0}$ 和 $y{1}$。其中 $\frac{\partial y{0}}{\partial w}=5$,$\frac{\partial y{1}}{\partial w}=2$。而 grad*tensors 设置两个 loss 对 w 的权重分别为 1 和 2。因此最终 w 的梯度为:
$$
\frac{\partial y{0}}{\partial w} \times 1+ \frac{\partial y_{1}}{\partial w} \times 2=9
$$
torch.autograd.grad()
1 | torch.autograd.grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False, only_inputs=True, allow_unused=False) |
功能:求取梯度。
- outputs: 用于求导的张量,如 loss
- inputs: 需要梯度的张量
- create_graph: 创建导数计算图,用于高阶求导
- retain_graph:保存计算图
- grad_outputs: 多梯度权重计算
torch.autograd.grad()的返回结果是一个 tuple,需要取出第 0 个元素才是真正的梯度。
下面使用torch.autograd.grad()求二阶导。在求一阶导时,需要设置 create_graph=True,让一阶导数 grad_1 也拥有计算图,然后再使用一阶导求取二阶导:
1 | x = torch.tensor([3.], requires_grad=True) |
输出为:
1 | (tensor([6.], grad_fn=<MulBackward0>),) |
需要注意的 3 点:
在每次反向传播求导时,计算的梯度不会自动清零。如果进行多次迭代计算梯度而没有清零,那么梯度会在前一次的基础上叠加。
代码示例:
1
2
3
4
5
6
7
8
9w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# 进行 4 次反向传播求导,每次最后都没有清零
for i in range(4):
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
y.backward()
print(w.grad)结果为:
1
2
3
4tensor([5.])
tensor([10.])
tensor([15.])
tensor([20.])每一次的梯度都比上一次的梯度多 5,这是由于梯度不会自动清零而在上一次计算的梯度结果上累加。应使用
w.grad.zero_()在每次梯度计算完后将梯度清零。1
2
3
4
5
6
7
8for i in range(4):
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
y.backward()
print(w.grad)
# 每次都把梯度清零
# w.grad.zero_()依赖于叶子节点的节点,requires_grad 属性默认为 True。
叶子节点不可执行
inplace操作。
以加法来说,``inplace 操作有a += x,a.add_(x),**改变后的值和原来的值内存地址是同一个**。非inplace 操作有a = a + x,a.add(x)`,改变后的值和原来的值内存地址不是同一个。
代码示例:
1 | print("非 inplace 操作") |
结果为:
1 | 非 inplace 操作 |
如果在反向传播之前 inplace 改变了叶子节点的值,再执行 backward() 会报错。
1 | w = torch.tensor([1.], requires_grad=True) |
这是因为在进行前向传播时,计算图中依赖于叶子节点的那些节点,会记录叶子节点的地址,在反向传播时就会利用叶子节点的地址所记录的值来计算梯度。比如在 $y=a \times b$ ,其中 $a=x+w$,$b=w+1$,$x$ 和 $w$ 是叶子节点。当求导 $\frac{\partial y}{\partial a} = b = w+1$,需要用到叶子节点 $w$。
2、逻辑回归 (Logistic Regression)
逻辑回归是线性的二分类模型。模型表达式:
$$
y=f(z)=\frac{1}{1+e^{-z}}
$$
其中 $z=WX+b$。$f(z)$ 称为 sigmoid 函数,也被称为 Logistic 函数。函数曲线如下:(横坐标是 $z$,而 $z=WX+b$,纵坐标是 $y$)。
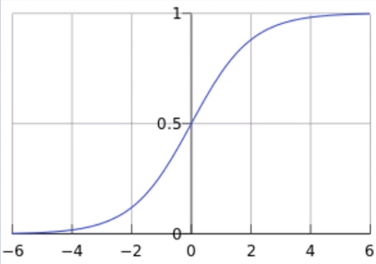
分类原则:当$y<0.5$时,类别为0(class=0);当 $0.5 \leq y$ 时,类别为 1(class=1)。
其中 $z=WX+b$ 就是原来的线性回归的模型。从横坐标来看,当 $z<0$ 时,类别为 0;当 $0 \leq z$ 时,类别为 1,直接使用线性回归也可以进行分类。逻辑回归是在线性回归的基础上加入了一个 sigmoid 函数,这是为了更好地描述置信度,把输入映射到 (0,1) 区间中,符合概率取值。
逻辑回归也被称为对数几率回归 $\ln \frac{y}{1-y}=W X+b$,几率的表达式为:$\frac{y}{1-y}$,$y$ 表示正类别的概率,$1-y$ 表示另一个类别的概率。根据对数几率回归可以推导出逻辑回归表达式:
$\ln \frac{y}{1-y}=W X+b$ $\frac{y}{1-y}=e^{W X+b}$ $y=e^{W X+b}-y * e^{W X+b}$ $y\left(1+e^{W X+b}\right)=e^{W X+b}$ $y=\frac{e^{W X+b}}{1+e^{W X+b}}=\frac{1}{1+e^{-(W X+b)}}$
PyTorch 实现逻辑回归

PyTorch 构建模型的 5 大步骤:
- 数据:包括数据清洗,数据读取,进行数据划分和数据预处理,比如读取图片如何预处理及数据增强。
- 模型:包括构建模型模块,组织复杂网络,初始化网络参数,定义网络层。
- 损失函数:包括创建损失函数,设置损失函数超参数,根据不同任务选择合适的损失函数。
- 优化器:包括根据梯度使用某种优化器更新参数,管理模型参数,管理多个参数组实现不同学习率,调整学习率。
- 迭代训练:组织上面 4 个模块进行反复训练。包括观察训练效果,绘制 Loss/ Accuracy 曲线,用 TensorBoard 进行可视化分析。
代码示例:
1 | import torch |
训练的分类直线的可视化如下:
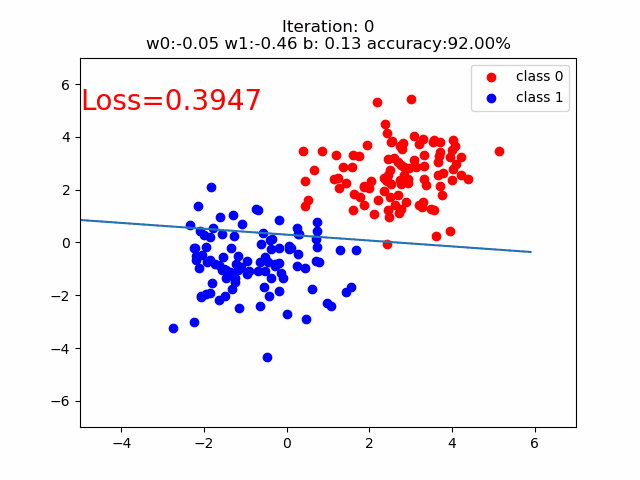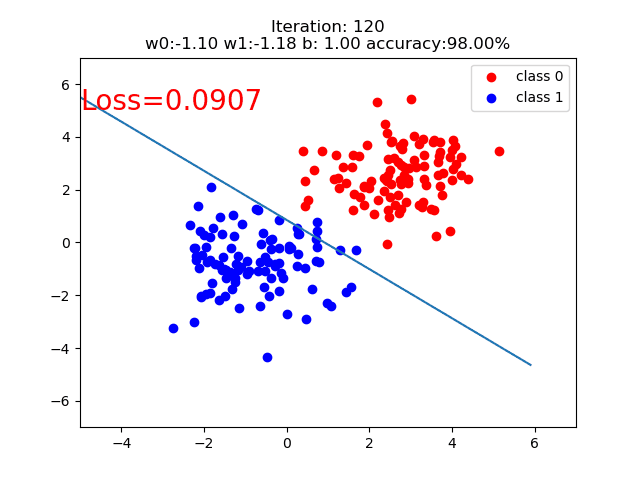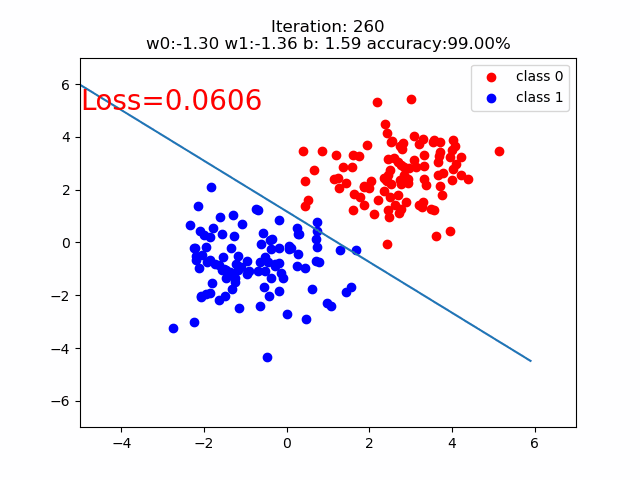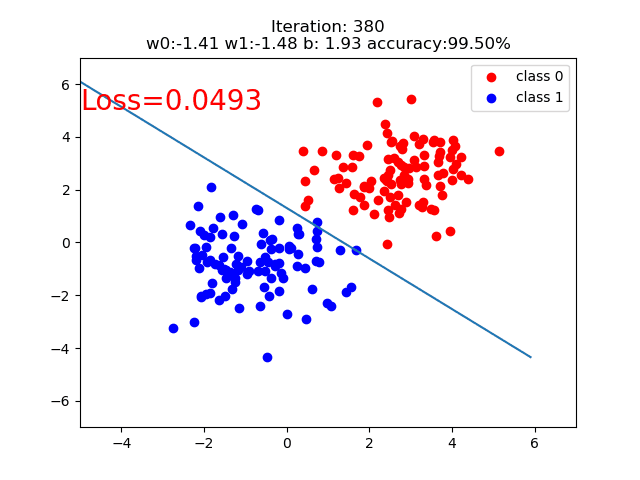
原文作者: 贺同学
原文链接: http://clarkhedi.github.io/2021/04/05/autograd-yu-luo-ji-hui-gui/
版权声明: 转载请注明出处(必须保留原文作者署名原文链接)