张量操作与线性回归

1、张量的操作

拼接

torch.cat()
1
torch.cat(tensors, dim=0, out=None)

功能：将张量按照 dim 维度进行拼接

  • tensors: 张量序列
  • dim: 要拼接的维度

代码示例：

1
2
3
4
t = torch.ones((2, 3))
t_0 = torch.cat([t, t], dim=0)
t_1 = torch.cat([t, t], dim=1)
print("t_0:{} shape:{}\nt_1:{} shape:{}".format(t_0, t_0.shape, t_1, t_1.shape))

输出是：

1
2
3
4
5
6
t_0:tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]]) shape:torch.Size([4, 3])
t_1:tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]]) shape:torch.Size([2, 6])
torch.stack()
1
torch.stack(tensors, dim=0, out=None)

功能：将张量在新创建的 dim 维度上进行拼接

  • tensors: 张量序列
  • dim: 要拼接的维度

代码示例：

1
2
3
4
5
6
7
t = torch.ones((2, 3))
# dim =2
t_stack = torch.stack([t, t, t], dim=2)
print("\nt_stack.shape:{}".format(t_stack.shape))
# dim =0
t_stack = torch.stack([t, t, t], dim=0)
print("\nt_stack.shape:{}".format(t_stack.shape))

输出为：

1
2
t_stack.shape:torch.Size([2, 3, 3])
t_stack.shape:torch.Size([3, 2, 3])

注：第一次指定拼接的维度 dim =2，结果的维度是 [2, 3, 3]。后面指定拼接的维度 dim =0，由于原来的 tensor 已经有了维度 0，因此会把tensor 往后移动一个维度变为 [1,2,3]，再拼接变为 [3,2,3]。

切分

torch.chunk()
1
torch.chunk(input, chunks, dim=0)

功能：将张量按照维度 dim 进行平均切分。若不能整除，则最后一份张量小于其他张量。

  • input: 要切分的张量
  • chunks: 要切分的份数
  • dim: 要切分的维度

代码示例：

1
2
3
4
a = torch.ones((2, 7))  # 7
list_of_tensors = torch.chunk(a, dim=1, chunks=3)   # 3
for idx, t in enumerate(list_of_tensors):
print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

输出为：

1
2
3
4
5
6
第1个张量：tensor([[1., 1., 1.],
        [1., 1., 1.]]), shape is torch.Size([2, 3])
第2个张量：tensor([[1., 1., 1.],
        [1., 1., 1.]]), shape is torch.Size([2, 3])
第3个张量：tensor([[1.],
        [1.]]), shape is torch.Size([2, 1])

注：由于 7 不能整除 3，7/3 再向上取整是 3，因此前两个维度是 [2, 3]，所以最后一个切分的张量维度是 [2,1]。

torch.split()
1
torch.split(tensor, split_size_or_sections, dim=0)

功能：将张量按照维度 dim 进行平均切分。可以指定每一个分量的切分长度。

  • tensor: 要切分的张量
  • split_size_or_sections: 为 int 时，表示每一份的长度，如果不能被整除，则最后一份张量小于其他张量；为 list 时，按照 list 元素作为每一个分量的长度切分。如果 list 元素之和不等于切分维度 (dim) 的值，就会报错。
  • dim: 要切分的维度

代码示例：

1
2
3
4
t = torch.ones((2, 5))
list_of_tensors = torch.split(t, [2, 1, 2], dim=1)
for idx, t in enumerate(list_of_tensors):
print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

结果为：

1
2
3
4
5
6
第1个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
第2个张量：tensor([[1.],
        [1.]]), shape is torch.Size([2, 1])
第3个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])

索引

torch.index_select()
1
torch.index_select(input, dim, index, out=None)

功能：在维度 dim 上，按照 index 索引取出数据拼接为张量 返回。

  • input: 要索引的张量
  • dim: 要索引的维度
  • index: 要索引数据的序号

代码示例：

1
2
3
4
5
6
7
# 创建均匀分布
t = torch.randint(0, 9, size=(3, 3))
# 注意 idx 的 dtype 不能指定为 torch.float
idx = torch.tensor([0, 2], dtype=torch.long)
# 取出第 0 行和第 2 行
t_select = torch.index_select(t, dim=0, index=idx)
print("t:\n{}\nt_select:\n{}".format(t, t_select))

输出为：

1
2
3
4
5
6
7
t:
tensor([[4, 2, 6],
        [6, 4, 0],
        [7, 3, 5]])
t_select:
tensor([[4, 2, 6],
        [7, 3, 5]])
torch.mask_select()
1
torch.masked_select(input, mask, out=None)

功能：按照 mask 中的 True 进行索引拼接得到一维张量 返回。

  • 要索引的张量
  • mask: 与 input 同形状的布尔类型张量

代码示例：

1
2
3
4
5
t = torch.randint(0, 9, size=(3, 3))
mask = t.le(5)  # ge is mean greater than or equal/   gt: greater than  le  lt
# 取出大于 5 的数
t_select = torch.masked_select(t, mask)
print("t:\n{}\nmask:\n{}\nt_select:\n{} ".format(t, mask, t_select))

结果为：

1
2
3
4
5
6
7
8
9
10
t:
tensor([[5, 5, 7],
        [2, 2, 8],
        [2, 6, 7]])
mask:
tensor([[ True,  True,  True],
             [False, False,  True],
             [False,  True,  True]])
t_select:
tensor([5, 5, 7, 8, 6, 7])

注：最后返回的是一维张量。

变换

torch.reshape()
1
torch.reshape(input, shape)

功能：变换张量的形状。当张量在内存中是连续时，返回的张量和原来的张量共享数据内存，改变一个变量时，另一个变量也会被改变。

  • input: 要变换的张量
  • shape: 新张量的形状

代码示例：

1
2
3
4
5
# 生成 0 到 8 的随机排列
t = torch.randperm(8)
# -1 表示这个维度是根据其他维度计算得出的(自动计算分配) [2x2x2=8]
t_reshape = torch.reshape(t, (-1, 2, 2))
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))

结果为：

1
2
3
4
5
6
7
t:tensor([1, 7, 2, 5, 3, 6, 0, 4])
t_reshape:
tensor([[[1, 7],
              [2, 5]],

            [[3, 6],
             [0, 4]]])

注：在上面代码的基础上，修改原来的张量的一个元素，新张量也会被改变。

代码示例：

1
2
3
4
5
# 修改张量 t 的第 0 个元素，张量 t_reshape 也会被改变
t[0] = 1024
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
print("t.data 内存地址:{}".format(id(t.data)))
print("t_reshape.data 内存地址:{}".format(id(t_reshape.data)))

结果为：

1
2
3
4
5
6
7
8
9
t:tensor([1024,    4,    3,    6,    5,    2,    7,    0])
t_reshape:
tensor([[[1024,    4],
              [   3,    6]],

            [[   5,    2],
             [   7,    0]]])
t.data 内存地址:2395125092288
t_reshape.data 内存地址:2395125089152
torch.transpose()
1
torch.transpose(input, dim0, dim1)

功能：交换张量的两个维度。常用于图像的变换，比如把c*h*w变换为h*w*c。

  • input: 要交换的张量
  • dim0: 要交换的第一个维度
  • dim1: 要交换的第二个维度

代码示例：

1
2
3
4
5
6
7
8
#把 c * h * w 变换为 h * w * c
t = torch.rand((2, 3, 4))
# print(t)
t_transpose_0 = torch.transpose(t, dim0=0, dim1=1)    # c*h*w   ->  h*c*w
# print(t_transpose_0)
t_transpose_1 = torch.transpose(t_transpose_0, dim0=1, dim1=2)   # c*h*w   ->  h*w*c
# print(t_transpose_1)
print("t shape:{}\nt_transpose shape: {}".format(t.shape, t_transpose_1.shape))

结果为：

1
2
t shape:torch.Size([2, 3, 4])
t_transpose shape: torch.Size([3, 4, 2])
torch.t()

功能：2 维张量转置，对于 2 维矩阵而言，等价于torch.transpose(input, 0, 1)。

torch.squeeze()
1
torch.squeeze(input, dim=None, out=None)

功能：压缩长度为 1 的维度。

  • dim: 若为 None，则移除所有长度为 1 的维度；若指定维度，则当且仅当该维度长度为 1 时可以移除。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
# 维度 0 和 3 的长度是 1
t = torch.rand((1, 2, 3, 1))
# 可以移除维度 0 和 3
t_sq = torch.squeeze(t)
# 可以移除维度 0
t_0 = torch.squeeze(t, dim=0)
# 不能移除 1
t_1 = torch.squeeze(t, dim=1)
print("t.shape: {}".format(t.shape))
print("t_sq.shape: {}".format(t_sq.shape))
print("t_0.shape: {}".format(t_0.shape))
print("t_1.shape: {}".format(t_1.shape))

结果为：

1
2
3
4
t.shape: torch.Size([1, 2, 3, 1])
t_sq.shape: torch.Size([2, 3])
t_0.shape: torch.Size([2, 3, 1])
t_1.shape: torch.Size([1, 2, 3, 1])
torch.unsqueeze()
1
torch.unsqueeze(input, dim)

功能：根据 dim 扩展维度，长度为 1。

2、张量的数学运算

主要分为：加减乘除，对数，指数，幂函数 和三角函数。

这里介绍一下常用的几种方法。

torch.add()
1
2
torch.add(input, other, out=None)
torch.add(input, other, *, alpha=1, out=None)

功能：逐元素计算 input + alpha * other。因为在深度学习中经常用到先乘后加的操作。

  • input: 第一个张量
  • alpha: 乘项因子
  • other: 第二个张量
torch.addcdiv()
1
torch.addcdiv(input, tensor1, tensor2, *, value=1, out=None)

计算公式为：out ${i}=\operatorname{input}{i}+$ value $\times \frac{\text { tensor } 1*{i}}{\text { tensor } 2*{i}}$

torch.addcmul()
1
torch.addcmul(input, tensor1, tensor2, *, value=1, out=None)

计算公式为：out ${i}=$ input ${i}+$ value $\times$ tensor $1*{i} \times$ tensor $2*{i}$

3、线性回归

线性回归是分析一个变量 ($y$) 与另外一 (多) 个变量 ($x$) 之间的关系的方法。一般可以写成 $y=wx+b$。线性回归的目的就是求解参数$w, b$。

线性回归的求解可以分为 3 步：

  1. 确定模型：$y=wx+b$
  2. 选择损失函数，一般使用均方误差 MSE：$\frac{1}{m} \sum*{i=1}^{m}\left(y*{i}-\hat{y}{i}\right)^{2}$。其中 $ \hat{y}{i} $ 是预测值，$y$ 是真实值。
  3. 使用梯度下降法求解梯度 (其中 $lr$ 是学习率)，并更新参数：
    • $w = w - lr * w.grad$
    • $b = b - lr * b.grad$

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)

lr = 0.05  # 学习率

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
# torch.randn(20, 1) 用于添加噪声
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)

# 构建线性回归参数
w = torch.randn((1), requires_grad=True) # 设置梯度求解为 true
b = torch.zeros((1), requires_grad=True) # 设置梯度求解为 true

# 迭代训练 1000 次
for iteration in range(1000):

    # 前向传播，计算预测值
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

    # 每次更新参数之后，都要清零张量的梯度
    w.grad.zero_()
    b.grad.zero_()

    # 绘图，每隔 20 次重新绘制直线
    if iteration % 20 == 0:

        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)

        # 如果 MSE 小于 1，则停止训练
        if loss.data.numpy() < 1:
            break

训练的直线的可视化如下：

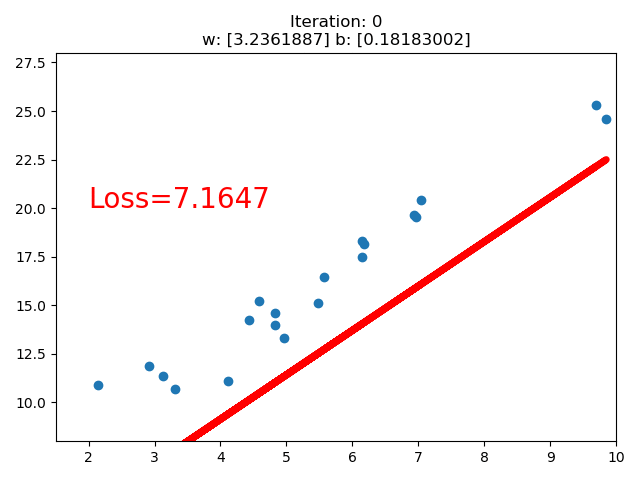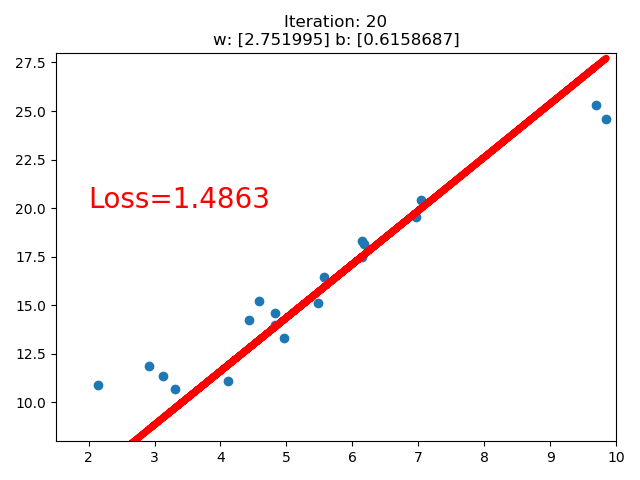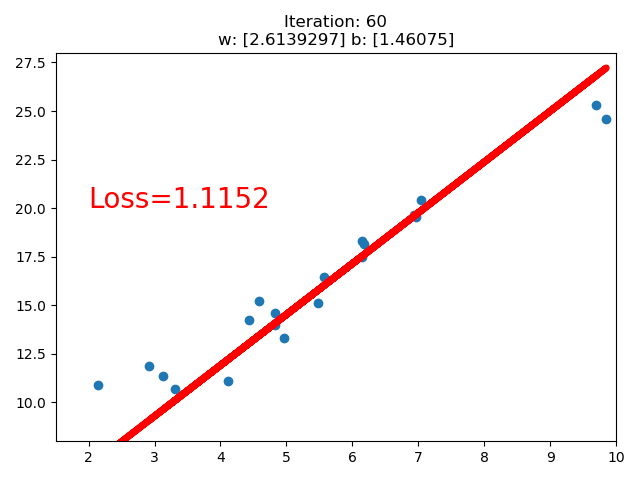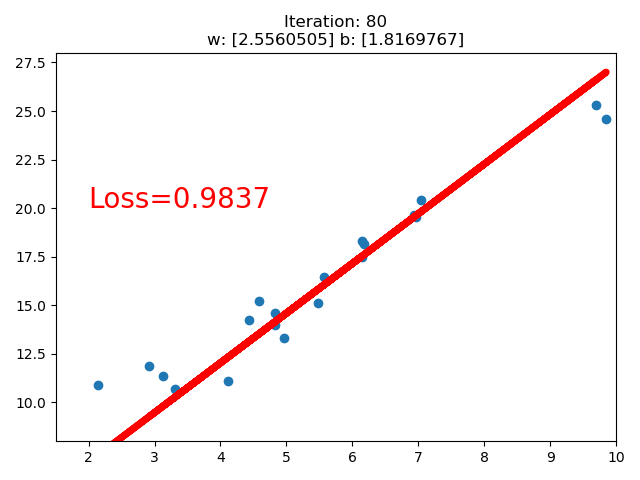
在 80 次的时候，Loss 已经小于 1 了，因此停止了训练。